01 질량과 속도
소리를 내는 모든 주체의 작용 방법에 대하여
Understanding the principle and workings of sonic manifestations produced by all subjective entities. [CLICK HERE TO READ THIS ARTICLE IN ENGLISH]
우리가 아는 유명한 물리학 공식에서는 힘, 질량 그리고 속도의 관계를 이야기합니다. 뉴튼은 힘을 질량과 가속력의 상관관계로 (F=ma), 아인슈타인은 에너지를 질량과 빛의 속도의 상관관계로 (E=mc2) 표현했습니다. 음악은 소리의 운동을 재료로 하는 예술 분야입니다. 소리는 멈추어 있지 않고 언제나 운동하며 드러나고 스러집니다. 첫번째 FfT에서는 질량과 속도와 관계된 간단한 물리적 이치를 들여다 봄으로써 소리의 작용을 탐구해 봅시다.
뉴튼과 아인슈타인의 두 공식 모두 하나의 질량을 가진 물체와 이에 더해진 속력으로 힘의 크기를 나타내는데, 그 하나의 질량은 즉 하나의 개체적 존재entity라고도 할 수 있습니다. 모든 독립체는 각자 자신의 중심을 갖고 있으므로 이 모두를 서로 다른 ‘주체 subjective entities’로 정의하고자 합니다. 이 개체적 존재가 지니는 또는 작용하는 힘의 크기는 그 존재의 질량과 운동의 속도에 따릅니다. 음악에서의 이 개체적 존재는 한 음이라고 할 수 있습니다. 따라서 모든 음은 질량과 속도를 가지고 그 힘의 작용을 이룬다고 할 수 있습니다.
한 음이 발현하는 과정은 눈에 보이지 않습니다. ‘드러나짐’은 드러나지 않은 힘의 작용, 그 반작용으로 생성됩니다. 보이지 않는 사람의 마음 속 동기가 행동을 일으키고, 보이지 않는 태엽의 기계작용이 보이는 시침과 분침을 움직여 시간을 알려 줍니다. 이러한 ‘현현’의 이면을 체體라고 하고 드러난 현상을 용用이라고 부릅니다. 동양, 특히 한국에서는 전통적으로 언제나 체용, 즉 본질과 현상의 유기적이고 역동적인 관계를 함께 묶어서 이해하고 사유하였습니다. 음-양, 이 양극은 고정적이며 이원적인 형이상학적 개념이 아니라 두 극점이 교차운동을 하며 이루는 물리적 운동이자 관계인 것입니다.
우리가 ‘음악’이라고 부르는 한 존재(an entity that is not a thing)는 소리로 현상계에 드러난 한 사건의 전체를 일컫습니다. 그 현상적 음악은 이를 연주하는 ‘주체’가 있으며 그 주체와 분리할 수 없습니다. 그 주체가 작용(체)을 하여 그 반작용으로 음악이라는 용用이 나오며 더 나아가 연주의 주체와 연주가 행해지는 시공간, 또한 청자들에 종속됩니다.
음악에 대한 종합적인 존재론적 논의를 잠시 멈추고 다시 행위자인 연주자에 주목 해봅시다. 연주자가 자신의 악기에 물리적으로 가하는 힘이 소리 에너지로 전환되어 하나의 음이 나오고, 그리고 이것이 시공에 중첩되고 이어지며 음악이라는 사건이 됩니다. 여기서 악기를 사실상 고정된 매개체라고 할 때에, 이를 조절하여 다양하게 조음하는 일은 연주자의 몫입니다. 우리가 말을 할 때에 딱딱한 입천장과 아래턱에 대對하여 혀와 입술을 조절하며 소리의 형形을 만들고, 호흡으로 공기의 압력을 조절하여 소리의 강유를 표현합니다.
물리 공식으로는 이러한 소리의 다채로운 예술적 형상들을 표현하기 어려울 것입니다. 그러나 공기의 압력에 의한 소리의 강유 즉 ‘힘’은 표현 가능합니다. 피아노를 예로 들자면 팔을 들어 손의 고도를 높여 위치 에너지를 증가시킬 수가 있습니다. 팔이 굵고 손이 무거운 사람은 상대적으로 적은 힘을 들여서 큰 소리를 낼 수 있겠지요. 이미 손 자체가 지닌 질량이 크기 때문입니다. 그렇지 않다면 손을 높이 들여 위치에너지를 높이는 것도 연주의 한 방법이 될 것입니다. 동시에 손이 최대한 중력을 타고 목표가 되는 지점에 도달할때에 그 위치에너지가 최대한 손실 없이 건반에 작용을 하겠지요. 특히 손이 낙하를 하는 동안 머뭇거린다면 목표지점에 떨어지며 다가갈때에 가속력으로 전환된 위치에너지의 힘을 잃게 됩니다. 자신감 있게 목표하는 지점에 가속력을 그대로 가해야 단단한 소리를 성공적으로 연주할 수 있게 되는 것입니다.
성악의 경우, 성대에 가해지는 공기의 압력의 세기에 따라 소리의 강유가 달라집니다. 그 압력은 질량을 가진 물체는 아니지만 시작과 끝이 있는 분명한 시공간 속 힘의 작용이므로 이를 또 하나의 개체적 존재로 해석하고자 합니다. 그 공기의 압력은 방향성을 가지고 이동을 하는 힘이 되는데 그것이 성대에 진동을 일으켜 소리를 발생시킵니다. 압력의 힘이 소리 에너지로 변환된 것입니다. 공기가 성대에 다가갈 수록 가해지는 압력은 빠르게 강해집니다.
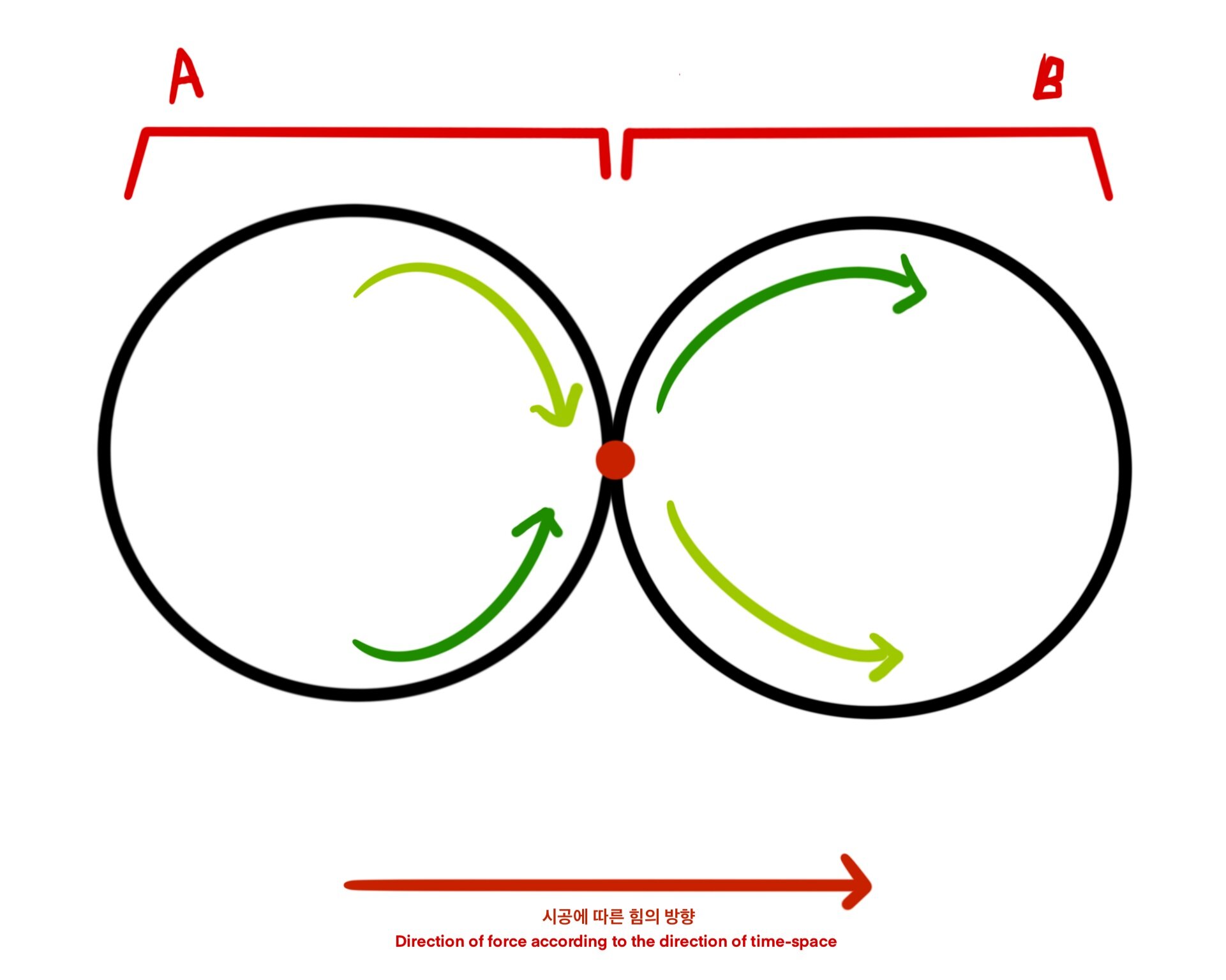
선회하는 소리의 수축과 팽창이자
소리 운동의 이면(체)과 현상(용)를 나타낸 도표
A = 체, B = 용 | A = 흡, B = 호
빨간 점 = 수축, 충돌지점
빨간 점 = 음音, B = 운韻
빨간 점 = 단, A & B = 장
위의 도표를 보면 A에 해당하는 부분은 소리가 드러나기 이전인 ‘체’이고 B는 소리가 현현하는 ‘용’의 부분입니다. A에서는 소리가 나기 이전에 일어나는 제반의 모든 운동 과정이 담겨있고, B는 가운데의 빨간 점 이후로 소리 에너지가 운동하는 방향을 말합니다. 가운데의 빨간 점은 공기가 성대에 닿아 소리로 변환되는 그 순간이며 피아노에서는 타건의 순간입니다. 노란색 화살표와 녹색 화살표는 각각 두 극점의 거리가 변화하는 모습을 나타내는데, 이는 손을 들어올려 피아노 건반과 손이라는 두 물체의 거리가 서로 멀어지다 다시 부딪히는 모습과 같습니다. 그리고 그 두 극점이 서로 당기어 만나면서 가속도가 붙고, 소리가 나오면서는 그 빠른 속도가 점점 느려지면서 두 극점 또한 멀어집니다. 빨간점에서 그 밀도가 극에 달했다가 소리가 허공에 소리의 밀도도 마찬가지로 희박해지겠죠.
이것이 바로 장단長短이자 호흡입니다. 두 극이 벌어져서 서로 멀어지는 과정은 길게 또는 시공이 팽창하다가 가까워지며 구심력이 작용하면서 빠르게 수축하며 결국 그 두 극이 만나 부딪힙니다. 이것이 단短인 것이고요. 장단의 시공간 수축과 팽창은 이렇게 호흡, 악기를 연주하여 소리를 내는 원리 그리고 국악에서 말하는 장단에까지 두루 통용되는 원리인 것입니다. 위 도표에서는 빨간 점이 ‘단短’이고 원으로 그려진 부분이 ‘장長’의 부분입니다. (A) 체에 해당하는 장은 구심력으로 수축短하는 장長이고 (B) 용에 해당하는 장長은 원심력으로 팽창하는 장입니다. 다시 (B)는 또 다른 체가 되어 또 다른 (B’)를 낳게 되겠죠.
이렇게 에너지-힘은 선회旋回합니다. 선율은 이렇게 음의 선회하는 운동을 정확하게 설명하는 단어입니다. 선율의 '선'자는 線(line)이 아니고 돌다, 선회한다는 뜻의 旋입니다. 두 극이 수축하여 교차하면서 부딪혀 소리를 만들고 그 소리가 다시 팽창하며 두 극이 멀어지다 또 다른 ‘소리’를 향해 수축하는 선회하는 운동이 일어난다는 뜻입니다. 오늘날 음악의 선율을 지각하는 일반적인 심상은 선line인것 같습니다. 선線을 닮은 선율은 기하적 도형보다 차원이 낮은 입체감이 없는 가느다란 물줄기와 같습니다. 그러나 본래 선율의 뜻은 3차원 시공에서 입체적으로 운동하는 소리의 고저장단의 율동 일체를 지시하는 단어인 것입니다. 선율, 즉 멜로디는 동서 막론하고 음률과 운율의 조화로 정의되는데, 위 도표에서 빨간 점으로 수축하는 부분이 ‘음音’에 해당하고 그 음이 선회하며 여음을 내는 것이 ‘운’입니다. 음운학에서 하나의 음절의 필수가결조건이 모음과 이에 붙는 자음입니다. 한글에서 초성과 종성이라는 말의 씨가 음을 주도하고, 이 음이 모음이라는 날줄에서 부딪쳐 울려 길게 울리는 것이 ‘운韻’인 것입니다. 음은 짧은 순간에 생겨나지만 운은 길게 늘일 수가 있습니다. 즉, 운은 길고, 음은 짧습니다. 음은 두 극이 서로 충돌하는 그 지점이고 운은 그 충돌의 결과로 이어지는 소리의 긴 울림인 것입니다.
이러한 선율의 선회하는 전 과정에 바로 가속력이 발견됩니다. 팽창하여 길게 늘어졌다 다시 수축할 때에 수축하는 지점에 다 다를 수록 중력 또는 인력의 작용이 커지면서 가속력이 증가합니다. 그리고 충돌 후에 서로 멀어질 때에도 처음에는 매우 빠르게 퍼져나가다 그 속력은 점차 줄어들게 됩니다. 악기나 성대에 가하는 힘, 압력이 강할 수록 수축 지점에서 강한 '충돌'이 일어납니다. 강한 충돌을 일으키는 힘은 두 물체의 질량 (위치에너지)과 속력에비례합니다. 그리고 얼마나 강한 힘이 그 수축과 충돌지점에 가해지는가에 따라 소리가 울리는 거리와 범위가 더 길고 넓어질 것입니다. 강한 충돌을 일으키기 위해서는, 성악가나 부는 악기 연주자라면라면 호흡의 밀도, 악기 연주자라면 악기의 줄이나 멤브레인의 장력, 손이나 활의 무게, 악기와 그 악기에 힘이 가해지는 손이나 체stick 간의 거리와 이로 인한 위치 에너지 등이 모두 고려되어야 할 물리적 조건일 것입니다.
이와 같이, 질량과 속도를 다루는 힘의 역학에 관한 방정식은 소리의 이면과 현상에 두루 작용합니다.
다음주에 발신하는 <02 기운생동> 편에서는 오늘 다룬 내용에 이어서 ‘기운생동’이라는 미학적 가치를 어떻게 위의 역학적 원리를 통하여 성취할 수 있는가, 또한 그 의의를 이야기해보고자 합니다. 감사합니다.